How To Calculate Maturity Value

Understanding the concept of maturity value is crucial when dealing with investments, loans, or financial instruments with a predetermined lifespan. This guide will delve into the intricacies of calculating maturity value, offering a comprehensive understanding of this fundamental financial concept. We'll explore the various factors that influence maturity value, provide step-by-step calculation methods, and offer practical examples to ensure a clear grasp of the topic.
The Essence of Maturity Value
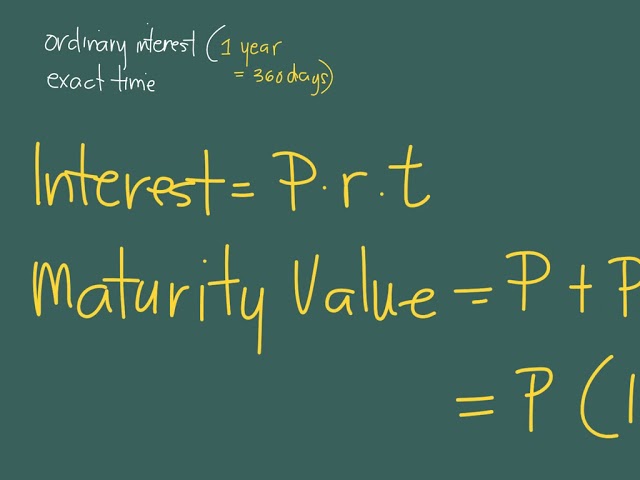
Maturity value, often referred to as the face value or par value, represents the amount an investor or borrower will receive or repay, respectively, upon the maturity or end date of a financial contract. This concept is integral to numerous financial instruments, including bonds, certificates of deposit (CDs), and loans, where the value of the investment or debt is specified upfront and paid back at a future date.
The calculation of maturity value is essential for financial planning, risk assessment, and investment decision-making. It allows investors to anticipate the potential returns and borrowers to plan their repayment strategies effectively. This knowledge is especially crucial in long-term investments or loans, where the maturity value can significantly impact overall financial outcomes.
Key Factors Influencing Maturity Value

The maturity value of a financial instrument is influenced by several key factors, each of which can affect the final amount payable at maturity. Understanding these factors is crucial for accurate calculations and financial forecasting.
Principal Amount
The principal amount, also known as the face value or par value, is the initial amount invested or borrowed. This value serves as the foundation for calculating the maturity value and remains unchanged throughout the life of the financial instrument. For instance, if an investor purchases a bond with a face value of \text{\textdollar}1,000, this amount will be the principal and the basis for calculating interest and final maturity value.
Interest Rate
The interest rate is a critical factor that determines the growth or cost of a financial instrument over time. It represents the percentage of the principal amount that is added or subtracted at regular intervals. In the case of investments, interest is typically added to the principal, increasing the overall value. Conversely, for loans, interest is subtracted from the principal, increasing the amount owed. The higher the interest rate, the greater the impact on the maturity value.
Compounding Frequency
The compounding frequency refers to how often interest is calculated and added to (or subtracted from) the principal amount. This can be annual, semi-annual, quarterly, monthly, or even daily. Compounding frequency significantly impacts the maturity value, as more frequent compounding leads to a higher final amount. For instance, a bond with annual compounding will have a lower maturity value than one with monthly compounding, assuming all other factors are equal.
Time to Maturity
The time to maturity, or the duration of the financial instrument, is another critical factor. The longer the time to maturity, the more opportunities there are for interest to accumulate, leading to a higher maturity value. This concept is particularly relevant for long-term investments and loans, where the impact of time on maturity value can be substantial.
Other Factors
While the above factors are the primary influences on maturity value, there may be other considerations depending on the specific financial instrument. These could include additional fees, penalties, or special features like call options on bonds. Understanding these unique factors is essential for an accurate maturity value calculation.
Step-by-Step Guide to Calculating Maturity Value
Calculating the maturity value involves a series of steps, each building upon the previous one. This process ensures an accurate determination of the final amount payable or receivable at maturity. Here’s a detailed guide:
Step 1: Identify the Principal Amount
Begin by identifying the principal amount, which is the initial investment or loan amount. This value is typically specified in the financial contract and remains constant throughout the instrument’s life.
Step 2: Determine the Interest Rate
Next, ascertain the interest rate associated with the financial instrument. This rate can be simple or compound, depending on the terms of the contract. Simple interest is calculated only on the principal amount, while compound interest is calculated on the principal and any accumulated interest.
Step 3: Establish the Compounding Frequency
Determine how often interest is compounded. This frequency can vary widely and is often specified in the financial contract. Common compounding frequencies include annually, semi-annually, quarterly, monthly, and daily.
Step 4: Calculate the Number of Compounding Periods
Using the compounding frequency and the time to maturity, calculate the number of compounding periods. This is a critical step as it determines how many times interest will be added or subtracted from the principal.
Formula: Number of Compounding Periods = Time to Maturity (in years) x Compounding Frequency
Step 5: Apply the Compound Interest Formula
With the principal amount, interest rate, compounding frequency, and number of compounding periods established, you can now apply the compound interest formula to calculate the maturity value.
Compound Interest Formula: Maturity Value = Principal Amount x [1 + (Interest Rate / Compounding Frequency)] ^ (Number of Compounding Periods)
Step 6: Consider Additional Factors
Depending on the financial instrument, there may be additional factors to consider. These could include fees, penalties, or special features. Ensure you account for these in your calculation to achieve an accurate maturity value.
Practical Example: Calculating Maturity Value for a Bond
Let’s walk through an example to illustrate the process of calculating maturity value. Imagine you’ve invested in a bond with the following characteristics:
- Principal Amount (Face Value): $\text{\textdollar}1,000$
- Interest Rate: $5\%$ annual
- Compounding Frequency: Semi-annually
- Time to Maturity: $5$ years
Step 1: Identify the Principal Amount
The principal amount, or face value, of the bond is \text{\textdollar}1,000.
Step 2: Determine the Interest Rate
The interest rate is 5\% annual.
Step 3: Establish the Compounding Frequency
The bond compounds interest semi-annually.
Step 4: Calculate the Number of Compounding Periods
Given the time to maturity of 5 years and the semi-annual compounding, the number of compounding periods is:
Number of Compounding Periods = $5$ years x $2$ semi-annual periods = $10$ periods
Step 5: Apply the Compound Interest Formula
Using the compound interest formula, we calculate the maturity value:
Maturity Value = $\text{\textdollar}1,000$ x [1 + ($5\%$ / $2$)] ^ $10$ = $\text{\textdollar}1,283.54$
So, at maturity, the bond's value will be $\text{\textdollar}1,283.54$, representing a return of $\text{\textdollar}283.54$ over the $5$-year period.
Advanced Calculations and Real-World Considerations

While the above example provides a straightforward illustration, real-world financial instruments can be more complex. In practice, you may encounter bonds with different structures, loans with variable interest rates, or investments with unique features. Each of these scenarios requires a tailored approach to calculating maturity value.
For instance, when dealing with variable interest rates, the calculation may need to account for changing rates over time. In such cases, a more dynamic approach, such as using an average interest rate or modeling potential rate changes, may be necessary. Similarly, for investments with call options, the maturity value calculation may need to consider the possibility of early redemption.
Conclusion: The Importance of Maturity Value Calculation
Calculating maturity value is a critical skill for anyone involved in financial planning, investment management, or loan administration. By understanding the factors that influence maturity value and following a systematic calculation process, investors and borrowers can make informed decisions and effectively manage their financial strategies. Whether it’s assessing the potential returns of an investment or planning for loan repayments, the ability to calculate maturity value is a cornerstone of sound financial management.
How does compounding frequency affect maturity value?
+Compounding frequency significantly impacts maturity value. More frequent compounding allows interest to accumulate more rapidly, leading to a higher final amount. For example, a bond with monthly compounding will have a higher maturity value than one with annual compounding, assuming all other factors are equal.
What happens if the interest rate changes over time?
+If the interest rate changes over time, the maturity value calculation becomes more complex. In such cases, you may need to use an average interest rate or model potential rate changes. This ensures that the calculation reflects the actual interest rates experienced over the life of the financial instrument.
Are there any limitations to the compound interest formula?
+While the compound interest formula is a powerful tool, it assumes a constant interest rate and regular compounding. In reality, financial instruments may have varying interest rates or irregular compounding periods. In such cases, more advanced financial models or simulations may be required to accurately estimate maturity value.